[클라우딩 어플리케이션 엔지니어링 TIL] TIL(Today I Learned) - Day15
들어가기전에
알고리즘 기초 공부를 하면서, 자바스크립트에서 어떻게 활용하는지에 대한 예시 문제와 함께 공부해본다.
강의를 보며 나의 주관적인 생각이 들어가 정리한것임으로 반드시 '내가 적은것이 맞다' 라는 것이 아니므로 읽어보시고 이상한부분이 있다면 저에게 알려주시거나 꼭 다른곳도 검색해서 찾아보기를 바랍니다.
목차
1. 학습 주제 ( 알고리즘 )
- 투포인터
- 백트레킹
- 동적 계획법
- 비트 마스크
2. 주요 메모 사항 소개
3. 공부하며 어려웠던 내용
학습 주제.1
투포인터, Two-Pointers
투포인터 또는 다중 포인터라고 불리우는 알고리즘이란,
- 일차원 배열에 두 개의 포인터를 두고 조작하는 알고리즘
- 배열에서 보통 이중 for문으로 O(N^2)에 처리되는 작업을 2개의 포인터의 움직임으로 O(N)에 해결
- 보통 연속적인 구간에 대한 계산을 할 때 많이 사용
* C언어의 포인터가 아니라 작업을 처리하기 위해 생성한 변수이다. 포인터라는 변수를 두개를 선언해서 투 포인터라고 부른다.
투포인터, 예시) 합이 5인 수열의 수 구하기

| 우선 두 포인터 모두 첫 번째 인덱스를 가리킨다. 아직 구간에 대한 합(partial Sum)이 7이고 구간 합이 10인 경우는 찾지 못한 상태 |
count = 0 partialSum = 7 p1 = 0 p2 = 0 |
 |
| 구간 합이 10을 넘지 못했기 때문에 두 번째 포인터를 증가시킴 해당 index에 대한 값을 구간 합 변수에 더해주어 partialSum 변수는 8이 된다. | count = 0 partialSum = 8 p1 = 0 p2 = 1 |
 |
| 아직 구간 합이 10을 넘지 않아서 두 번째 포인터를 증가시키고 이제 구간 합이 11이 된다. | count = 0 partialSum = 11 p1 = 0 p2 = 2 |
 |
| 구간 합이 10을 넘었기 때문에 이번엔 반대로 첫 번째 포인터를 증가시키면서 기존 값을 partialSum에서 빼준다. | count = 0 partialSum = 4 p1 = 1 p2 = 2 |
 |
| 이번엔 두 번째 포인터를 증가시키며, 구간 합도 더한다. | count = 0 partialSum = 9 p1 = 1 p2 = 3 |
 |
| 마찬가지로 또 두 번째 포인터를 증가시킴 구간 합이 10이 되었기 때문에 count 변수증가 |
count = 1 partialSum = 10 p1 = 1 p2 = 4 |
 |
| 다음 수가 0일 수도 있기 때문에 이번에도 두 번째 포인터를 증가시킴 | count = 1 partialSum = 14 p1 = 1 p2 = 5 |
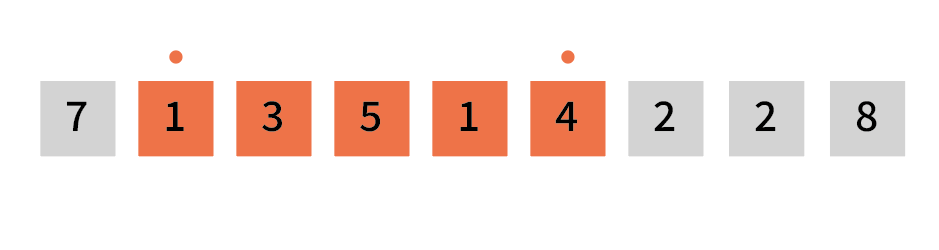 |
| 구간 합이 10을 넘었기 때문에 첫 번째 포인터 증가시킴 | count = 1 partialSum = 13 p1 = 2 p2 = 5 |
 |
| 또 다시 첫 번째 포인터 증가시키며, 구간 합이 10이 되었기 때문에 count 증가시킴 | count = 2 partialSum = 10 p1 = 3 p2 = 5 |
 |
| 두 번째 포인터를 증가시킴 | count = 2 partialSum = 12 p1 = 3 p2 = 6 |
 |
| 첫 번째 포인터를 증가시킴 | count = 2 partialSum = 7 p1 = 4 p2 = 6 |
 |
| 두 번째 포인터를 증가시킴 | count = 2 partialSum = 9 p1 = 4 p2 = 7 |
 |
| 또 한번 두 번째 포인터를 증가시킴 | count = 2 partialSum = 17 p1 = 4 p2 = 8 |
 |
| 두 번째 포인터가 끝에 도달했기 때문에 이 후로 첫 번째 포인터만 계속 증가시킴 | count = 2 partialSum = 16 p1 = 5 p2 = 8 |
 |
| 첫 번째 포인터를 증가시킴 | count = 2 partialSum = 12 p1 = 6 p2 = 8 |
 |
| 첫 번째 포인터를 증가시키며, 구간 합이 10이 되었기 때문에 count를 증가시킴 | count = 3 partialSum = 10 p1 = 7 p2 = 8 |
 |
| 모든 포인터가 끝에 도달함으로써 종료된다. | count = 3 partialSum = 8 p1 = 8 p2 = 8 |
 |
학습 주제.2
백트레킹, BackTracking
가능한 모든 후보해를 탐색하면서 해결책을 찾아가는 알고리즘 기법 중 하나
- 백트래킹은 완전 탐색(Exhaustive Search)의 일종으로, 해를 찾을 때까지 모든 가능한 경우의 수를 탐색 포인터의 움직임으로 O(N)에 해결하는 알고리즘이다.
- 주로 탐색(Search) 문제나 결정 문제(Decision Problem)를 해결하는 데 사용
백트레킹 알고리즘의 일반적인 절차
- 선택 : 주어진 선택지 중에서 다음 단계로 진행할 선택을 하여 해의 후보를 만듭니다.
- 조건 검사 : 선택된 후보가 문제의 조건을 만족하는지 검사합니다.
- 해결책 탐사 :
- 조건을 만족하면 선택된 후보를 해로 인정하고, 다음 단계로 진행합니다.
- 조건을 만족하지 않으면 이전 상태로 되돌아가 다른 선택지를 시도합니다.
- 결과 확인 : 모든 선택지를 검사한 후에도 해결책을 찾지 못했으면 실패로 처리합니다.
백트레킹, 예시) 순열(Permutation) 구하기
자바스크립트에서 백트래킹을 구현하려면 재귀 함수를 이용하여 탐색을 수행합니다.
각 단계마다 선택을 하고 조건을 검사한 후에 해당 선택이 유효하면 다음 단계로 이동하고, 유효하지 않으면 이전 상태로 되돌아갑니다.
function backtrack(permutation, nums, result) {
if (permutation.length === nums.length) {
result.push(permutation.slice());
return;
}
for (let num of nums) {
if (!permutation.includes(num)) {
permutation.push(num);
backtrack(permutation, nums, result);
permutation.pop();
}
}
}
function permute(nums) {
const result = [];
backtrack([], nums, result);
return result;
}
// 테스트
const nums = [1, 2, 3];
console.log(permute(nums)); // [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
학습 주제.3
동적 계획법, Dynamic Programming
동적(Dynamic)이란? 자료구조에서 동적 할당(Dynamic Allocation)은 프로그램이 실행되는 도중에 실행에 필요한 메모리를 할당하는 기법을 의미지만 반면 동적 계획법에서 동적은 별다른 의미 없이 사용된 단어
주어진 문제를 여러 하위 문제로 나누어 해결한 후, 그 결과를 저장하고 재활용하여 전체 문제의 해를 구하는 알고리즘 기법
- 메모리를 적절히 사용하여 수행 시간의 효율성을 비약적으로 향상하는 방법
- 주로 최적화(Optimization) 문제나 조합 문제 등에서 사용
- 동적 계획법은 주로 다음과 같은 특성을 가지는 문제에 적용
- 하위 문제의 해결 결과를 재활용할 수 있는 경우
- 문제가 중복되는 하위 문제를 갖고 있는 경우
동적 계획법 접근 방법
- 하향식 접근법(Top-down Approach): 재귀적인 방식으로, 큰 문제를 해결하기 위해 작은 하위 문제를 호출하는 방법입니다. 이 과정에서 중복되는 하위 문제의 해결 결과를 캐시하여 중복 계산을 피합니다.
- 상향식 접근법(Bottom-up Approach): 반복적인 방식으로, 작은 하위 문제부터 시작하여 큰 문제를 해결하는 방법입니다. 작은 문제부터 해결하여 중복 계산을 피합니다.
동적 계획법, 예시) 피보나치 수열 구하기
function fibonacci(n) {
const dp = [0, 1]; // 기초값 설정
for (let i = 2; i <= n; i++) {
// 이전 두 수의 합을 계산하여 저장
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n]; // n번째 피보나치 수 반환
}
// 테스트
console.log(fibonacci(5)); // 5
console.log(fibonacci(10)); // 55
console.log(fibonacci(15)); // 610
학습 주제.4
비트 마스크, Bitmask
- 특정 알고리즘은 아니고 비트 연산을 이용한 일종의 코딩 기법
- 이진수가 자료 구조로 사용된다.
- 이진법 성징을 이용하여 문제를 해결하는 방법
- 배열 대신 이진수를 이용할 수 있다.
ex) [true, ture, false, true] = 13(1101) - 굉장히 빠르고 메모리 사용량이 적다.
- 그리디, 동적 계획법 등 다른 알고리즘과 함께 사용할 수 있다.
* 비트 연산자 : 비트를 직접 조작하는 연산자
비트를 배열(집합)처럼 사용하기
| false로 초기화 하기 | bit = 0; |
| N개 만큼 true로 초기화하기 | bit = (1 << N) -1; |
| i번째 요소 true로 바꾸기 | bit |= (1 << i); |
| i번째 요소 false로 바꾸기 | bit &= ~(1 << i); |
| i번째 요소 토글하기 | bit ^= (1 << i); |
| i번째 요소 true인지 체크하기 | bit & (1 << i); |
두 집합끼리 연산하기
| 합집합 | A | B; |
| 교집합 | A & B; |
| A에서 B를 뺀 차집합 | A & (~B); |
| 합집합에서 교집합 제외(xor) | A ^ B |
주의할 점
- 정수형 범위를 넘지 않도록 조심할 것 (JS에서도 비트 연산은 정수 범위를 넘을 수 없다)
- 연산자 우선 순위에 주의할
주요 메모 사항 소개
투포인터
일차원 배열에 두 개의 포인터를 두고 조작하는 알고리즘
백트레킹
가능한 모든 후보해를 탐색하면서 해결책을 찾아가는 알고리즘
동적계획법
주어진 문제를 여러 하위 문제로 나누어 해결한 후, 그 결과를 저장하고 재활용하여 전체 문제의 해를 구하는 알고리즘
공부하면서 어려웠던 내용
알고리즘 활용법
실전문제나 예제들을 보았을 때, 지금까지 배웠던 알고리즘에서 이걸로 푼다면 좋겠다! 싶어서 작성하다가도 중간에 길을 잃어버린다거나 뭔가 잘 안되는거 같은 느낌이 들때가 있다 그리고 찾아보면 더 쉽게 푸는 방법이 있었구나 ! 생각을 하게되고, 쉽게 풀 수 있는것도 배우고 더 많은걸 알아가다보니 되려 머리가 더 복잡해져서 못푸는 경향이 생기고있다. 내 머릿속에서 정리정돈이 안 돼서 이런 일이 일어나는것 같아서 차분히 하나하나 잘 되새겨 봐야겠다.
참고문헌 사이트